I have been reading the paper, "Bibliometric analysis and systematic literature review of the traffic paradoxes (1968–2022)," co-authored by Jia Yao, Ziyi Cheng, and Anthony Chen, published recently in the journal Transportation Research B, 177 (2023) 102832. It contains a very thorough, exhaustive compendium and analysis of a plethora of traffic paradoxes, beginning with the classical Braess Paradox (1968) paper. I had the honor of translating the 1968 paper from German to English, along with Dietrich Braess and my then PhD student Tina Wakolbinger. The translation, "On a paradox of traffic planning was published in Transportation Science in 2005, along with a preface that I wrote with David Boyce.
Below is a photo taken with Professor Dietrich Braess and Tina Wakolbinger, when we hosted him at the Isenberg School of Management after our translation was published in 2006.
The Braess Paradox has inspired many researchers from different disciplines and, over the years, I have written several papers on this paradox and others, which I have co-authored with both PhD students and other collaborators.
In the study by Yao, Cheng, and Chen, I was thrilled and humbled to see that I am the "top leading author with a minimum of five publications" on traffic paradoxes and that I am in some amazing scholarly company.
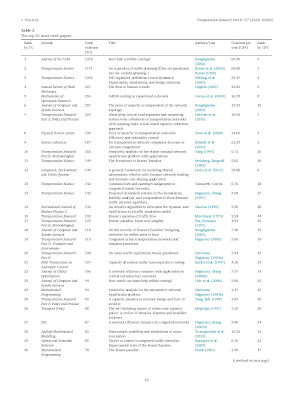
I have had the pleasure of working on paradoxes and the authors of this Transportation Research B bibliometric study have listed the top 50 cited papers, which include not only the translation paper of ours but also my work with my PhD advisor (now deceased) Stella Dafermos, Ding Zhang, and Qiang "Patrick" Qiang.
Below is a list of the 50 most cited papers that the authors compiled.
References
Braess, D., 1968. Über ein paradoxon aus der verkehrsplanung. Unternehmensforschung 12 (1), 258–268.
Braess, D., Nagurney, A., Wakolbinger, T., 2005. On a paradox of traffic planning. Transportation Science 39 (4), 446–450.
Dafermos, S., Nagurney, A., 1984a. On some traffic equilibrium theory paradoxes. Transportation Research B 18 (2), 101–110.
Dafermos, S., Nagurney, A., 1984b. Sensitivity analysis for the asymmetric network equilibrium problem. Mathematical Programming 28 (2), 174–184.
Nagurney, A., 2000. Congested urban transportation networks and emission paradoxes. Transportation Research D 5 (2), 145–151.
Nagurney, A., 2010. The negation of the Braess paradox as demand increases: the wisdom of crowds in transportation networks. EPL (Europhysics Letters) 91 (4), 48002.
Nagurney, A., Qiang, Q., 2007a. A network efficiency measure for congested networks. EPL 79 (3), 38005.
Nagurney, A., Qiang, Q., 2007b. Robustness of transportation networks subject to degradable links. EPL (Europhysics Letters) 80 (6), 68001.
Nagurney, A., Qiang, Q., 2008a. An efficiency measure for dynamic networks modeled as evolutionary variational inequalities with application to the internet and vulnerability analysis. Netnomics 9 (1), 1–20.
Nagurney, A., Qiang, Q., 2008b. A network efficiency measure with application to critical infrastructure networks. Journal of Global Optimization 40 (1–3), 261–275.
Nagurney, A., Zhang, D., 1997. Projected dynamical systems in the formulation, stability analysis, and computation of fixed-demand traffic network equilibria. Transportation Science 31, 147–158.
Nagurney, L.S., Nagurney, A., 2016. Physical proof of the occurrence of the Braess paradox in electrical circuits. EPL (Europhysics Letters) 115, 28004.
And, in 2007, a paper that I co-authored with Patrizia Daniele, who was supported by Radcliffe as my collaborator, and with David Parkes (now Dean of SEAS at Harvard) was published! Full citation:
Nagurney, A., Parkes, D.C., Daniele, P. 2007. The Internet, evolutionary variational inequalities, and the time-dependent Braess paradox. Computational Management Science 4(4): 355-375.
Posts
